题意
给你一个数字序列S,再给一个数字序列pattern,S和pattern中的数字都是1到s(s<=25)。每个序列里的数字都有个排名,也就是第几小,现在我们要用pattern来匹配S。在本题中匹配是指每个数字的
排名都一样,即同是第k小,最后输出匹配的所有位置。
思路
KMP好题,对KMP的理解又透彻了一点点~ 我们考虑两个字符串A,B 在此题中,A[1],A[2],…,A[k]与B[1],B[2],…,B[k]匹配条件:
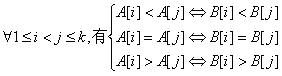
若A[1],A[2],…,A[k-1]与B[1],B[2],…,B[k-1]匹配,则加上A[k]与B[k]仍然匹配的条件是:
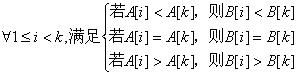
必须在与k无关的时间复杂度内完成该操作 然而,由于A[1],A[2],…,A[k-1]与B[1],B[2],…,B[k-1]已经匹配,可以简化比较操作 考虑到字符集很小(不超过25),我们可以定义以下几个变量:
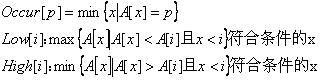
Occur[p],Low[i],High[i]可能不存在,若存在则取最小的符合条件的x 则A[1],A[2],…,A[k-1]与B[1],B[2],…,B[k-1]匹配,加上A[k]与B[k]仍然匹配的条件可简化为:
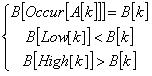
接下来就可以用O(SK)时间内预处理求出Occur[p],Low[i],High[i],然后套用kmp算法,总时间复杂度为O(N+SK)
代码
[cpp] #include <iostream> #include <cstdio> #include <cmath> #include <algorithm> #include <string> #include <cstring> #include <vector> #include <set> #include <stack> #include <queue> #define MID(x,y) ((x+y)/2) #define MEM(a,b) memset(a,b,sizeof(a)) #define REP(i, begin, end) for (int i = begin; i <= end; i ++) using namespace std; typedef long long LL; int n, k, s; int S[100005], pattern[25005]; int low[25005], high[25005], ranks_pos[30], next[100005]; vector <int> ans; void init(){ MEM(ranks_pos, -1); MEM(low, -1); MEM(high, -1); for (int i = 0; i < k; ++ i){ int j = pattern[i] - 1; while(j){ if (~ranks_pos[j]){ low[i] = j; break; } j --; } j = pattern[i] + 1; while(j < s+1){ if (~ranks_pos[j]){ high[i] = j; break; } j ++; } if (ranks_pos[pattern[i]] == -1) ranks_pos[pattern[i]] = i; } } bool check(int A[], int B[], int k, int pos){ if (~ranks_pos[A[pos]]){ if (B[k+ranks_pos[A[pos]]] != B[k+pos]) return false; } if (~low[pos] && ~ranks_pos[low[pos]]){ if (B[k+ranks_pos[low[pos]]] >= B[k+pos]) return false; } if (~high[pos] && ~ranks_pos[high[pos]]){ if (B[k+ranks_pos[high[pos]]] <= B[k+pos]) return false; } return true; } void get_next(){ int j = -1; next[0] = -1; for (int i = 1; i < k; ++ i){ while(j > -1 && !check(pattern, pattern, i-j-1, j+1)) j = next[j]; if (check(pattern, pattern, i-j-1, j+1)) j ++; next[i] = j; //printf("next%d = %d\n", i, next[i]); } } void kmp(){ ans.clear(); get_next(); int j = -1; for (int i = 0; i < n; ++ i){ while(j > -1 && !check(pattern, S, i-j-1, j+1)) j = next[j]; if (check(pattern, S, i-j-1, j+1)) j ++; if (j == k - 1){ ans.push_back(i - k + 1); j = next[j]; } } } int main(){ while(scanf("%d %d %d", &n, &k, &s) != EOF){ for (int i = 0; i < n; i ++) scanf("%d", &S[i]); for (int i = 0; i < k; i ++) scanf("%d", &pattern[i]); init(); kmp(); printf("%d\n", ans.size()); for (int i = 0; i < (int)ans.size(); ++ i){ printf("%d\n", ans[i]+1); } } return 0; } [/cpp]
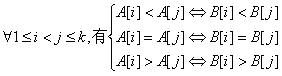 若A[1],A[2],…,A[k-1]与B[1],B[2],…,B[k-1]匹配,则加上A[k]与B[k]仍然匹配的条件是:
若A[1],A[2],…,A[k-1]与B[1],B[2],…,B[k-1]匹配,则加上A[k]与B[k]仍然匹配的条件是: 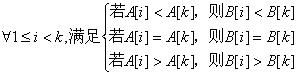 必须在与k无关的时间复杂度内完成该操作 然而,由于A[1],A[2],…,A[k-1]与B[1],B[2],…,B[k-1]已经匹配,可以简化比较操作 考虑到字符集很小(不超过25),我们可以定义以下几个变量:
必须在与k无关的时间复杂度内完成该操作 然而,由于A[1],A[2],…,A[k-1]与B[1],B[2],…,B[k-1]已经匹配,可以简化比较操作 考虑到字符集很小(不超过25),我们可以定义以下几个变量: 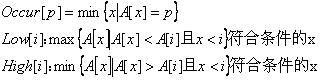 Occur[p],Low[i],High[i]可能不存在,若存在则取最小的符合条件的x 则A[1],A[2],…,A[k-1]与B[1],B[2],…,B[k-1]匹配,加上A[k]与B[k]仍然匹配的条件可简化为:
Occur[p],Low[i],High[i]可能不存在,若存在则取最小的符合条件的x 则A[1],A[2],…,A[k-1]与B[1],B[2],…,B[k-1]匹配,加上A[k]与B[k]仍然匹配的条件可简化为: 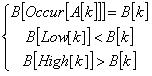 接下来就可以用O(SK)时间内预处理求出Occur[p],Low[i],High[i],然后套用kmp算法,总时间复杂度为O(N+SK)
接下来就可以用O(SK)时间内预处理求出Occur[p],Low[i],High[i],然后套用kmp算法,总时间复杂度为O(N+SK)